Módulo 3: Conceitos matemáticos e metodologias para ensinar crianças surdas (Livro Digital)
| Site: | IFSC |
| Curso: | Repositório de Recursos Educacionais Digitais |
| Livro: | Módulo 3: Conceitos matemáticos e metodologias para ensinar crianças surdas (Livro Digital) |
| Impresso por: | Guest user |
| Data: | Wednesday, 17 Dec 2025, 18:00 |
Índice
- Apresentação do Módulo
- 1. O ensino de Matemática na educação bilíngue de surdos
- 2. Conceitos matemáticos e metodologias para ensinar crianças surdas
- 3. Conteúdos e Metodologias para o ensino de matemática nos anos iniciais em um ambiente bilíngue (Libras-português)
- 3.1 Sugestões de atividades para Educação Infantil
- 3.1.1 Atividades para crianças entre 4 e 6 anos
- 3.2 Sugestões de atividades para os Anos Iniciais
- 3.2.1 Ensinando sobre Números
- 3.2.2 Sistema de Numeração Decimal
- 3.2.3 Ensinando Adição
- 3.2.4 Ensinando Subtração
- 3.2.5 Ensinando Multiplicação
- 3.2.6 Ensinando Divisão
- 3.2.7 Ensinando as Horas
- 4. Uso de tecnologias educacionais para o ensino da matemática
- Considerações Finais
- Referências
- Ficha Técnica
1. O ensino de Matemática na educação bilíngue de surdos
Ao pensarmos sobre o ensino de matemática na educação bilíngue de surdos podemos nos perguntar: por onde começar?
Precisamos começar pela BNCC - Base Nacional Comum Curricular.
“A Base Nacional Comum Curricular (BNCC) é um documento de caráter normativo que define o conjunto orgânico e progressivo de aprendizagens essenciais que todos os alunos devem desenvolver ao longo das etapas e modalidades da Educação Básica, de modo a que tenham assegurados seus direitos de aprendizagem e desenvolvimento, em conformidade com o que preceitua o Plano Nacional de Educação” (Brasil, 2018, p.7).
Segundo a proposta da BNCC, os conceitos matemáticos
“[...] podem contribuir para o desenvolvimento do pensamento computacional dos alunos, tendo em vista que eles precisam ser capazes de traduzir uma situação dada em outras linguagens, como transformar situações-problema, apresentadas em língua materna, em fórmulas, tabelas e gráficos e vice-versa” (Brasil, 2018, p.271, grifo nosso).
Esse pressuposto nos leva ao fato de que a situação matemática deve ser apresentada à criança surda na sua primeira língua, a língua de sinais.
De acordo com a BNCC (Brasil, 2018), os conhecimentos matemáticos são importantes para a utilização no convívio social e para a formação de sujeitos críticos. Aprender matemática não se resume a contar, medir, compreender grandezas ou utilizar números. Ela possibilita formular “sistemas abstratos, que organizam e inter-relacionam fenômenos do espaço, do movimento, das formas e dos números, associados ou não a fenômenos do mundo físico. Esses sistemas contêm ideias e objetos que são fundamentais para a compreensão de fenômenos, a construção de representações significativas e argumentações consistentes nos mais variados contextos” (p.265).
1.1 A matemática na Educação infantil
Como você já deve saber, na Educação Infantil não há divisão por disciplinas ou conteúdos.
De acordo com as Diretrizes Curriculares Nacionais da Educação Infantil - DCNEI (Brasil, 2009), em seu Artigo 9º, os eixos estruturantes das práticas pedagógicas dessa etapa da Educação Básica são as interações e a brincadeira.
Na BNCC (Brasil, 2018), a organização curricular da Educação Infantil está estruturada em campos de experiências, que “[...] constituem um arranjo curricular que acolhe as situações e as experiências concretas da vida cotidiana das crianças e seus saberes, entrelaçando-os aos conhecimentos que fazem parte do patrimônio cultural” (p.40).
Um desses campos diz respeito a Espaços, tempos, quantidades, relações e transformações. As crianças, no seu dia a dia, se deparam com experiências que exigem contagem, ordenação, relações entre quantidades, dimensões, medidas, comparação de pesos e de comprimentos, avaliação de distâncias, reconhecimento de formas geométricas, conhecimento e reconhecimento de numerais cardinais e ordinais etc., que são, essencialmente, conhecimentos matemáticos.
No quadro abaixo temos alguns dos objetivos de aprendizagem e desenvolvimento que a BNCC propõe para a Educação Infantil, separados por faixa etária, mais diretamente ligados ao conhecimento matemático.
Quadro 01 - Objetivos do campo de experiências “Espaços, tempos, quantidades, relações e transformações”

Fonte: adaptado da BNCC (Brasil, 2018, p.51)
Mas, como esses objetivos podem ser alcançados? Precisamos pensar metodologias de ensino para a matemática para as crianças se apropriarem desses conceitos desde a educação infantil.
1.2 A Matemática no Ensino Fundamental - anos iniciais
A passagem da criança da Educação Infantil para o Ensino Fundamental não pode ser abrupta. Privilegiar as situações lúdicas no Ensino Fundamental I fará a articulação com as experiências vividas pela criança na Educação Infantil. Desse modo, um bom planejamento irá proporcionar tanto “[...] a progressiva sistematização dessas experiências quanto o desenvolvimento, pelos alunos, de novas formas de relação com o mundo, novas possibilidades de ler e formular hipóteses sobre os fenômenos, de testá-las, de refutá-las, de elaborar conclusões, em uma atitude ativa na construção de conhecimentos” (Brasil, 2018, p.57).
No ensino fundamental, os processos matemáticos, que envolvem a resolução de problemas, a investigação, os projetos e modelagens são estratégias necessárias para a aprendizagem da matemática, e auxiliam no desenvolvimento do letramento matemático, que envolve processos de raciocínio, representação, comunicação e argumentação (Brasil, 2018), ou seja, como a criança organiza seu aprendizado da matemática com base na análise de situações da vida cotidiana, de outras áreas do conhecimento e da própria Matemática.
Os processos matemáticos [...] podem ser citados como formas privilegiadas da atividade matemática, motivo pelo qual são, ao mesmo tempo, objeto e estratégia para a aprendizagem ao longo de todo o Ensino Fundamental [...] (Brasil, 2018, p.266).
Em resumo, segundo a BNCC:
[...] recursos didáticos como malhas quadriculadas, ábacos, jogos, livros, vídeos, calculadoras, planilhas eletrônicas e softwares de geometria dinâmica têm um papel essencial para a compreensão e utilização das noções matemáticas. Entretanto, esses materiais precisam estar integrados a situações que levem à reflexão e à sistematização, para que se inicie um processo de formalização (Brasil, 2018, p.276).
Visando o desenvolvimento desses aspectos, as competências específicas para o ensino fundamental objetivam:

Fonte: adaptado da BNCC (Brasil, 2018, p.267)
Para ampliar seus conhecimentos, sugerimos que você estude as primeiras páginas que tratam da área de matemática na BNCC.
Nelas estão os fundamentos e a proposta das habilidades que devem ser ensinadas em Matemática. Assim, você será capaz de entender o contexto e o porquê de cada objeto do conhecimento/habilidade proposta em cada etapa do ensino fundamental.
BNCC - área de matemática2. Conceitos matemáticos e metodologias para ensinar crianças surdas
Como vimos, a BNCC propõe que o aluno seja capaz de encontrar soluções para os problemas, aplicando os conhecimentos matemáticos no seu cotidiano. Para isso, o trabalho com a matemática precisa ir além da memorização de conceitos e fórmulas. Precisa possibilitar ao aluno o desenvolvimento da criatividade, a participação ativa, acesso a ambientes e materiais que permitam questionar, refletir, problematizar e explorar todas as suas potencialidades (Campos; Oliveira, 2020).
O aprendizado da matemática inicia desde cedo, nas brincadeiras, na interação com outras pessoas, em situações familiares cotidianas. As crianças surdas, especialmente aquelas filhas de pais ouvintes, perdem oportunidades de aprender nas situações do dia a dia pela ausência da linguagem.
“[...] Crianças surdas podem ficar fora de discussões relacionadas ao tamanho das roupas, dos sapatos e outros, limitando assim sua exposição a oportunidades de aprendizagem matemática. Também podem não ter acesso à televisão e outras formas de comunicação que poderiam dar-lhes informação relacionada com matemática. Outro ponto importante é a falta de comunicação linguística com seus pais, irmãos e outros membros da família, bem como a sociedade em geral. Situações como comprar algo na padaria e realizar o cálculo para descobrir o troco são comuns entre crianças ouvintes e incomuns entre crianças surdas” (Vargas; Dorneles, 2013, p.414).
A surdez por si só não causa atraso na aprendizagem, mas a ausência de linguagem e de interações sociais pode dificultar o desenvolvimento se não houver uma intervenção adequada (Nogueira; Borges; Frizzarini, 2013). Assim como as crianças ouvintes, as crianças surdas precisam vivenciar situações de aprendizagem que favoreçam a aquisição dos conceitos matemáticos através da interação e da resolução de problemas em atividades cotidianas.
De acordo com os autores, para a construção do conhecimento matemático, três questões precisam ser consideradas:
1) a utilização da língua de sinais;
2) metodologias de ensino que favoreçam experiências significativas;
3) ambientes, recursos e situações de aprendizagem que auxiliem o aluno a utilizar a matemática em diferentes contextos.

Com relação às metodologias de ensino, Campos e Oliveira (2020, p.10) sugerem:
1) metodologias que explorem o aspecto visual;
2) metodologias que despertem o interesse do aluno;
3) metodologias que situem o aluno como protagonista de seu aprendizado.
Essas metodologias, além de favorecerem a aprendizagem das crianças surdas, também são importantes para o aprendizado das crianças ouvintes.
As metodologias visuais podem ser trabalhadas através da utilização de materiais concretos, recursos tecnológicos e jogos que favoreçam a apropriação dos conceitos matemáticos.
A resolução de problemas, investigação de situações matemáticas, questões do cotidiano podem estimular o interesse do aluno, contribuindo para o desenvolvimento cognitivo e promovendo uma aprendizagem mais contextualizada.
Atividades nas quais os alunos participem de forma ativa, sendo responsáveis em pensar soluções e possibilidades de resolução para as questões apresentadas favorecem a elaboração do raciocínio lógico-matemático.
2.1 Construção dos conceitos matemáticos na Educação Infantil
Segundo a BNCC, “a Educação Infantil precisa promover experiências nas quais as crianças possam fazer observações, manipular objetos, investigar e explorar seu entorno, levantar hipóteses e consultar fontes de informação para buscar respostas às suas curiosidades e indagações” (Brasil, 2018, p.43).
Diferente da criança ouvinte que, em geral, tem no âmbito familiar de seu dia a dia, todo esse contexto favorável proposto pela BNCC, chegando “pronta” para a escola, a criança surda não costuma ter vivências que “favoreçam a construção de conceitos matemáticos informais, como, por exemplo, a memorização da sequência de palavras-número, que muito cedo é conhecida das crianças ouvintes” (Nogueira; Borges; Frizzarini, 2013, p.167).
Segundo Kamii (2015, p.65)
[...] a criança não constrói o número fora do contexto geral do dia a dia. Portanto, o professor deve encorajar a criança a colocar todos os tipos de coisas, ideias e eventos em relação o tempo todo, em vez de focar apenas na quantificação.
O professor pode propor situações escolares nas quais as crianças utilizem os números relacionados à vida diária ou às brincadeiras e jogos em grupo.
A quantificação constitui uma parte inevitável da vida diária, como, por exemplo, distribuir copos de papel e guardanapos, dividir objetos igualmente entre as crianças, guardar peças de jogos de tabuleiros, dentre muitas outras.
Já os jogos em grupo proporcionam um contexto excelente para o desenvolvimento do pensamento geral e para a comparação de quantidades. É importante variar os tipos de jogos: jogos com alvos, jogos de esconder, jogos de corrida, jogos de pegar, jogos de adivinhações, jogos de tabuleiro e baralho etc.
Em 2021, a Diretoria de Políticas de Educação Bilíngue de Surdos - DIPEBS, vinculada ao Ministério da Educação - MEC, lançou um material com seis cadernos, que compõem uma Proposta Curricular para o Ensino de Português Escrito como Segunda Língua para Estudantes Surdos da Educação Básica e do Ensino Superior.
E, por que estamos falando de um material de português em um curso de matemática?
Simplesmente porque o português escrito como segunda língua é fundamental para os surdos se apropriarem e aprofundarem o conhecimento das outras disciplinas. Além disso, especificamente para a educação infantil, não há distinção entre disciplinas, logo, o caderno I desse material, que trata da educação infantil, é duplamente rico para quem vai atuar nessa etapa da educação com crianças surdas.
Recomendamos a leitura completa desse material.
 Caderno I - Educação infantil
Caderno I - Educação infantilVamos apresentar aqui algumas sugestões propostas no Caderno I, mas recomendamos que você faça a leitura completa do material.
Em relação ao objeto do conhecimento: Noção de tempo, noção de espaço, pode-se, por exemplo, relacionar conceitos básicos de tempo como: agora, antes, durante, depois, ontem, hoje, amanhã, e de modo, tais como: lento, rápido, depressa, devagar etc, por meio de imagens de contos, fábulas ou lendas.
Lembra da história A Lebre e a Tartaruga, na qual a lebre desafia a tartaruga para uma corrida? É uma boa história para você apresentar às crianças os conceitos lento, rápido, depressa, devagar. Você encontra o texto da fábula A Lebre e a Tartaruga, de Esopo, e também o vídeo em Libras disponível on-line e de forma gratuita.
Diversos gêneros textuais trabalham a noção de tempo de forma evidente. Assim, sua utilização em diferentes momentos da sala de aula, através de contação de histórias em Libras ou utilizando textos escritos, ajudam a criança a se apropriar dos conceitos.
Identificar relações espaciais como dentro, fora, embaixo, na frente, atrás, acima, abaixo, entre e do lado, por meio de imagens de tirinhas, de histórias de livros paradidáticos, de poemas visuais ou através de brincadeiras, como a amarelinha ou circuitos com bambolê.

Ao final da Educação infantil espera-se que a criança consiga:
- Associar o sinal dos algarismos em Libras com os algarismos indo-arábicos em situações que eles aparecem no cotidiano: número de telefone, endereço, placa de carro, documentos, idade, altura ou peso de si própria e de pessoas da família, ou ainda de personagens de histórias.
- Utilizar a datilologia com o recurso de memorização em brincadeiras que envolvam os números e sua representação pelos algarismos.
- Repetir os números através da sua representação em Libras e a representação gráfica dos algarismos.
- Articular a datilologia de forma clara, com um ritmo lento, a fim de ser bem compreendido pelo interlocutor, em situações dialógicas estabelecidas a partir de imagens, número escrito e que aparecem em textos trabalhados.
- Executar práticas da sequência numérica por meio da Libras.
- Relatar fatos importantes sobre seu nascimento e desenvolvimento; a história dos seus familiares, de sua comunidade, histórias de contos, fábulas e lendas conhecidas, por meio de registros gráficos (desenhos, palavras e frases) com atenção para os números que aparecem nestes contextos.
- Representar, pela escrita numérica, brincadeiras cotidianas, por exemplo, escrever com giz, no chão; com caneta, no quadro; com pincel, em cartaz, para registro de pontuação de jogos.
2.2 Conceitos da matemática nos anos iniciais
Para o ensino de Matemática nos anos iniciais, a BNCC propõe cinco unidades temáticas, que orientam a formulação de habilidades a serem desenvolvidas ao longo do Ensino Fundamental. São elas:
1) Números;
2) Álgebra;
3) Geometria;
4) Grandezas e medidas; e
5) Probabilidade e estatística.
Obviamente não conseguiremos tratar aqui de todos os aspectos de todas elas, então traremos algumas e as relacionaremos de forma mais direta com pesquisas e propostas de metodologias e materiais voltados para crianças surdas.
Uma observação importante que precisamos fazer sobre a Libras e os números é a sua característica da transparência, ou seja, de se escrever como se fala, o que não acontece nas línguas orais.
Os elementos dos números escritos podem ser identificados a partir dos sinais em Libras. Por exemplo, o número “duzentos e um” é traduzido em Libras, pela justaposição dos sinais 201 igual à escrita 201.
Já na língua oral, o número “duzentos e um” se fosse escrito em numerais da maneira como é “falado” oralmente ficaria “2001” e não 201, de acordo com o valor posicional dos números.
Segundo Silva (2008, p.208),
[...] Os surdos não se deparam com esta situação. Eles se apropriam de imediato da escrita convencional dos números para, num outro momento, compreenderem que em nosso sistema de numeração a quantidade de algarismos se vincula à magnitude do número representado e que o valor do número é determinado pela posição que cada algarismo ocupa – valor posicional [...] (Silva, 2008, p.208).
Esse fato favorece a criança surda no momento em que ela escreve como se fala, de modo que ela irá se deparar com “as regras operatórias específicas da escrita numérica arábica posicional, composta por dígitos e regras de composição multiplicativa e aditiva das diversas unidades. Estas últimas terão sua conceitualização formulada de outra maneira, num outro momento [...]”, no momento do português escrito (Silva, 2008, p.214).
Para que você, professor, possa se apropriar dos conceitos matemáticos que são trabalhados com as crianças no ensino fundamental, compartilhamos os cadernos de matemática desenvolvidos pelo MEC (Ministério da Educação) para o programa Gestar I, que foi um programa de formação continuada realizado em 2008, orientado para a formação continuada de professores que atuam nos anos iniciais do Ensino Fundamental, objetivando a melhoria do processo de ensino aprendizagem da matemática.
Entendemos que é uma referência riquíssima para você estudar, revisar e consolidar seu conhecimento matemático como professor deste nível de ensino.
Saiba mais:
Neste material, os autores trabalham os diversos campos da matemática – Aritmética, Álgebra, Geometria, Estatística e Probabilidade e propõem situações didáticas que visam “[...] garantir que os alunos relacionem observações empíricas do mundo real a representações (tabelas, figuras e esquemas) e associem essas representações a uma atividade matemática (conceitos e propriedades), fazendo induções e conjecturas, fazendo com que desenvolvam a capacidade de identificar oportunidades de utilização da matemática para resolver problemas, aplicando conceitos, procedimentos e resultados para obter soluções e interpretá-las segundo os contextos das situações [...]” (Brasil, 2018, p.265).
Programa Gestão da Aprendizagem Escolar - Gestar I
Cadernos de teoria e prática (TP)
TP1 - Planejando o Ensino de Matemática
TP2 - Número Natural: conceito e representação
TP3 - Operações com Números Naturais
TP6 - Números Racionais: conceito e representação
TP8 - Operação com números Racionais
Programa Gestão da Aprendizagem Escolar - Gestar I
Cadernos de atividades de apoio à aprendizagem (AAA)
AAA1 - Número Natural: conceito e representação
AAA2 - Operações com Números Naturais
2.2.1 Desenvolvimento do pensamento numérico
Segundo a BNCC,
“A unidade temática Números tem como finalidade desenvolver o pensamento numérico, que implica o conhecimento de maneiras de quantificar atributos de objetos e de julgar e interpretar argumentos baseados em quantidades. No processo da construção da noção de número, os alunos precisam desenvolver, entre outras, as ideias de aproximação, proporcionalidade, equivalência e ordem, noções fundamentais da Matemática. Para essa construção, é importante propor, por meio de situações significativas, sucessivas ampliações dos campos numéricos. No estudo desses campos numéricos, devem ser enfatizados registros, usos, significados e operações” (Brasil, 2018, p.268).
Nesta unidade temática, uma das habilidades sugeridas envolve registros verbais e simbólicos, sendo possível, na perspectiva bilíngue, trabalhar com a língua de sinais, o português escrito, símbolos matemáticos e registro escrito dos números.

A figura a seguir mostra um exemplo de atividade que pode ser desenvolvida com as crianças para trabalhar os números e a contagem de objetos.
Figura 1 - Soma e identificação da quantidade em Libras

Fonte: Oliveira; Dionysio (2023)
Segundo Oliveira e Dionysio (2023), utilizando um material como o apresentado na figura, “[...] é possível que os alunos tenham contato com a configuração de mãos, que representam os números. Dessa maneira, podem ser desenvolvidas estratégias de contagem, comparação entre quantidades, indicação de valores iguais, maiores e menores” (p.13)
Essa proposta vai ao encontro da sugestão apresentada pela BNCC para o desenvolvimento de habilidades no primeiro ano:
(EF01MA03) estimar e comparar quantidades de objetos de dois conjuntos (em torno de 20 elementos), por estimativa e/ou por correspondência (um a um, dois a dois) para indicar “tem mais”, “tem menos” ou “tem a mesma quantidade”.
Na pesquisa desenvolvida por Zanqueta e Nogueira (2017), as autoras confirmaram a hipótese de que, propor perguntas desafiadoras aos surdos, através de diálogos em Libras, possibilita alcançar ganhos qualitativos de pensamento.
Como a escola é o único local em que os surdos podem exercer sua língua de maneira plena, acreditávamos que a perspectiva dialógica da abordagem metodológica com o cálculo mental possibilitaria aos alunos trocas simbólicas praticamente inexistentes nas atividades educacionais cotidianas (Zanqueta; Nogueira, 2017, p.64).
No artigo, as autoras descrevem as atividades propostas com números e contagem utilizando o sistema de numeração decimal (SND), as respostas dos alunos e as análises e conclusões que puderam tirar delas. Por exemplo:
Ao ser solicitada pela professora/pesquisadora a prosseguir a contagem a partir de 798, Maria iniciou: “799, 799”, e ficou parada por uns instantes, balançando a cabeça como se não soubesse, até que sinaliza “7100”. Ampliamos o questionamento para o grupo e Luísa sinalizou: “800” e João ficou observando um pouco e só depois da resposta de Luísa, respondeu, sem muita convicção: “800”.
Esta situação, entre outras semelhantes, nos demonstrou que Maria necessitava de atividades específicas que favorecessem a (re)construção do SND, bem como o “auxílio” de recursos didáticos [...] (Zanqueta; Nogueira, 2017, p.70).
Em outro momento as autoras descrevem como “Luísa” explica qual era o número que vinha depois de 999:
[...] Luísa sinalizou 99 com a mão esquerda e encostando a mão direita, sinaliza rapidamente 0, 1, 2, ..., 9 (indicando 990, 991, 992,..., 999) e então, sinaliza 1.000 (sinal por sinal, inclusive o ponto). Pudemos inferir que o seguinte teorema em ação foi mobilizado por Luísa: Para descobrir o próximo número da sequência basta acrescentar mais uma unidade ao último anunciado. Nesse exemplo, fica claro as possibilidades pedagógicas da Libras no ensino do SND, pois os algarismos de um numeral, ao serem explicitados em Libras, são distribuídos espacialmente em suas posições, permitindo que a criança visualize diretamente o local de cada um desses algarismos do numeral, ao passo que, na língua oral, a criança precisa relacionar uma palavra (novecentos, por exemplo), com a posição do algarismo 9 no numeral (Zanqueta; Nogueira, 2017, p.76).
Nessa perspectiva, os alunos surdos são incentivados a explorar números maiores que a primeira ordem de milhar, a trabalhar a passagem da numeração falada para a escrita de números, a exercer a contagem, tanto progressiva quanto regressiva, com números que exigem mudança de ordem ou de classe, como passar do 999 para o 1000, em sua primeira língua, a Libras, obtendo ganhos reais em relação ao sistema de numeração decimal que utilizamos.
No decorrer do artigo, as autoras também tratam do cálculo mental, usando essa metodologia dialogada em Libras para problemas do campo aditivo.
Observe a representação em Libras do número 9.000 de duas maneiras:
Figura 2 - Representação em Libras do número 9.000

Fonte: Zanqueta; Nogueira (2017, p.67)
Ao fazer a datilologia algarismo por algarismo, qualquer pessoa poderá identificar esse número, no entanto sinalizando nove mil, somente quem conhece a Libras entenderá, ajudando o sujeito surdo a se apropriar do valor posicional do sistema numérico, principalmente no que se refere a números de maior valor.
Ao finalizar a pesquisa as autoras constataram que:
[...] a dinâmica instaurada de cálculo mental (dialógica) favoreceu a troca de ideias e o desenvolvimento da autonomia, proporcionando um avanço qualitativo do raciocínio; aumentou a coragem em enfrentar desafios e criar novos processos de cálculos (novo pelo menos para o aluno); aumentou a capacidade de concentração dos alunos nas aulas; concorreu para a compreensão do conceito e dos diferentes significados do número; favoreceu o domínio de números de ordens elevadas; colaborou para a compreensão, o enriquecimento e a flexibilização dos procedimentos algorítmicos (Zanqueta; Nogueira, 2017, p.85).
Saiba mais
Você conhece o canal MathLibras? Ele é fruto de um projeto desenvolvido na Universidade Federal de Pelotas (UFPel), onde acontece uma parceria importantíssima entre o Departamento de Educação Matemática e a Área de Libras do Centro de Letras e Comunicação, para a produção de vídeos com conteúdos de matemática em Libras.
No canal encontramos coleções de vídeos em Libras que tratam dos conceitos de comparação e classificação, que a criança precisa desenvolver, pois fazem parte da construção do conceito de número. A coleção sobre comparação é voltada para a criança surda, já a coleção de vídeos sobre classificação é voltada para a utilização do professor.
Vale a pena conhecer o material que o canal disponibiliza! Seguem os links para que você possa conhecer o material e também explorar os demais vídeos do canal.
3. Conteúdos e Metodologias para o ensino de matemática nos anos iniciais em um ambiente bilíngue (Libras-português)
Smole (2019, online) organiza as noções matemáticas que as crianças precisam aprender, a partir da educação infantil, em quatro eixos:
1. conhecimento dos números, dos seus significados e das operações entre eles;
2. conhecimento de formas geométricas, localização espacial e desenvolvimento corporal;
3. conhecimento das principais grandezas e medidas;
4. interpretação e organização de dados a partir dos primeiros contatos com o tratamento da informação.
A noção de número é construída pela criança de forma progressiva. A capacidade de contar depende de a criança conseguir coordenar diferentes ações sobre os objetos, que são: classificação, inclusão, seriação, correspondência e conservação (Piaget; Szeminska, 1981). Apenas saber contar os números em sequência não significa que a criança construiu a noção de número.
Para consolidar essa noção, a criança precisa também compreender a noção de espaço, de tempo e de causalidade.
A construção da noção de espaço e tempo são essenciais para o conhecimento da realidade. As primeiras estruturas mentais se constroem em função das coordenações do corpo no espaço e das sequências temporais das ações (Silva; Frezza, 2010).
Na prática!
Para orientar a realização de atividades práticas que trabalham a construção do conceito de número com crianças da educação infantil, a pesquisadora Pamela Paola Leonardo elaborou um caderno didático-pedagógico para professores.
O caderno apresenta sequências didáticas que exploram os conceitos de classificação, inclusão, seriação, correspondência e conservação.
As atividades sugeridas foram pensadas para trabalhar com crianças que se encontram no período pré-operatório, conforme as etapas propostas por Piaget.
Caderno didático-pedagógico: construção do conceito de número
3.1 Sugestões de atividades para Educação Infantil
A criança pequena ressignifica objetos e suas representações de situações da vida diária ao classificá-los em forma de listas, a partir de atributos como tamanho, peso, cor, forma, em Libras e em português escrito. Ou, ao relacionar objetos, seja em miniaturas ou reais, com os locais onde se encontram no cotidiano - objetos da sala, objetos da cozinha, objetos do banheiro, objetos do supermercado, objetos da rua, sempre em Libras, primeiramente, e depois em português escrito.

Outra situação do dia a dia vivida pela criança é a de relacionar números à quantidade de crianças. Por exemplo: quantidade de meninas e meninos ou de presentes e ausentes na aula do dia e de objetos da mesma natureza, como: bonecas, bolas, livros etc. Este tipo de vivência pode ocorrer no dia a dia de uma sala de aula ou por meio de imagens acompanhadas de português escrito em histórias contadas, listas, cardápios, diários.

É possível ainda propor que a criança organize objetos reais conforme suas respectivas cores fazendo correspondências: colocar objetos amarelos na caixa amarela, azuis na caixa azul, ou separar figuras geométricas por cores e organizá-las.

O professor também pode pedir que a criança identifique objetos e pessoas em imagens a partir de informações específicas como, por exemplo: o que a figura representa, o que está na frente e o que está atrás, o que está em cima, o que está embaixo, o que está em movimento, o que está parado, o que está mais colorido ou não.

Ao ser exposta a cardápios, listas, relatos, contos, fábulas, histórias infantis, lendas, rótulos de embalagens, a criança se depara com a necessidade de contar objetos e pessoas por meio da leitura de algarismos e da escrita de números. A partir desses materiais, ela poderá fazer a identificação da quantidade por meio da exploração de objetos concretos e dos registros gráficos, tais como: sinais “+” e “-”, “maior” e “menor”, “mais” e “menos”.

O mesmo acontece ao relacionar imagens e desenhos com sinais e palavras em atividades lúdicas, como nos jogos de memória, dominó, quebra-cabeça, sacola surpresa.

Todas essas atividades sugeridas podem ser desenvolvidas já na educação infantil ou no primeiro ano do ensino fundamental para que as crianças possam compreender a importância dos números no cotidiano, bem como se apropriar de conceitos da matemática que serão ampliados no decorrer do ensino fundamental.
3.1.1 Atividades para crianças entre 4 e 6 anos
Com as crianças mais velhas da educação infantil, entre 4 e 6 anos, as atividades já podem ser mais específicas.
As crianças maiores já podem identificar números em situações cotidianas como, por exemplo, número de telefone, numeração de roupa, número de sapato, e perceber a função do número para quantificar e identificar coisas.
Relacionar números às suas respectivas quantidades registradas em português escrito em cardápios, listas, receitas, regras de jogos e brincadeiras, rótulos de embalagens e nas histórias, contos e fábulas. Identificar o número anterior, o número posterior ou o que esteja entre dois números, em uma sequência numérica, em jogos e brincadeiras mediadas pela Libras, em textos visuais e em português escrito.

A criança deve ser incentivada a observar, receitas, regras de jogos e brincadeiras, rótulos de embalagens, agendas, bilhetes, convites, listas, para perceber que apresentam informações que se utilizam de letras e da escrita dos numerais.
Nesse processo, a criança conseguirá distinguir o número, a escrita do número e a quantidade e começará a identificar os números em situações do cotidiano, como por exemplo, número de telefone, número da roupa, número do sapato, números em documentos, números nas placas dos automóveis.

Em relação às questões do espaço, a criança deve ser incentivada a orientar-se em relação aos objetos, às pessoas e ao seu próprio corpo em: brincadeiras, jogos com regras organizadas por letras, ou palavras impressas em português escrito, por exemplo: DIREITA ou ESQUERDA.
Ao brincar, a criança aprende a seguir orientações: ‘para cima’, ‘para o lado esquerdo’, ‘para trás’, e também seguir as regras de jogos e brincadeiras estabelecidas em português escrito. Aprende a fazer relações espaciais como: ‘dentro x fora’, ‘em cima x embaixo’, ‘acima x abaixo’, ‘entre x do lado’, ‘longe x perto’ por meio de representações figurativas de objetos e de representações esquemáticas, gráficas ou tridimensionais.

As crianças também devem ser expostas a atividades que lhes permitam observar medidas, como quantidade de passos, palmos da mão, polegadas etc., expressas por meio de múltiplas linguagens: desenho, gráficos, registro por números ou escrita espontânea e em diferentes gêneros textuais relacionados ao tema.
É possível incluir medidas de peso, altura em gráficos básicos construídos em conjunto com as crianças nas situações de rotina em sala de aula. Por exemplo: gráfico da altura, do peso dos alunos, do peso dos produtos.

Ao localizar, em rótulos de embalagens, informações como pesos, medidas e prazos de validade do produto ou reproduzindo posições no espaço, a partir de figuras acompanhadas de representações escritas da Libras e em português escrito por exemplo: ‘embaixo da cadeira’, ‘em cima da mesa’, ‘do lado da professora’, ‘atrás da porta’, a criança vai ganhando a compreensão da função social do registro escrito e a finalidade de textos, conhecimento de mundo e conhecimento da escrita.
Situações ocorridas em sala de aula, em casa, assim como em fatos narrados nas contações de histórias são facilitadores para que a criança possa identificar relações temporais como antes, durante e depois.

Atividades escritas de rotina realizadas em sala de aula, como no calendário, e também em gêneros textuais, agendas, bilhetes, cartas e convites, ajudam a estabelecer a noção de tempo de dia, mês, ano, semana, ontem, hoje, amanhã, antes, depois.

Saiba mais
Sugerimos a leitura do artigo As crianças e o conhecimento matemático: experiências de exploração e ampliação de conceitos e relações matemáticas, escrito por Priscila Monteiro e publicado nos Anais do I Seminário Nacional: Currículo em movimento, realizado em Belo Horizonte em 2010.
Nele, a autora problematiza o ensino da matemática na educação infantil e discute possibilidades para o trabalho pedagógico nessa área do conhecimento. Apresenta também sugestões de atividades que podem ser realizadas para trabalhar os conceitos matemáticos.
As crianças e o conhecimento matemático3.2 Sugestões de atividades para os Anos Iniciais
Boaler (2020, p. 80) destaca que “mesmo quando trabalhamos em uma questão aritmética simples, cinco áreas diferentes do cérebro estão envolvidas, e duas delas são rotas visuais”.
Considerando esse potencial visual que o cérebro humano tem para a resolução de questões matemáticas e a Libras como uma língua visuoespacial, faz sentido pensar que o ensino da Matemática deve ser pautado em questões visuais, especialmente considerando um público cuja língua natural tem essa característica.
O autor ressalta ainda que, com o estímulo certo, todos podem aprender uma Matemática de alto nível. Nesse sentido, argumenta que “Se os cérebros podem mudar em três semanas, imagine o que pode acontecer em um ano de aulas de matemática se os alunos receberem os materiais certos e mensagens positivas sobre seu potencial e sua capacidade” (Boaler, 2018, p. 4).
Nos anos iniciais, a utilização de materiais concretos, que a criança possa pegar e manusear, bem como materiais visuais que facilitem a compreensão, são extremamente relevantes para potencializar a aprendizagem.
Para os estudantes surdos, ainda são poucos os materiais pensados diretamente para o ensino da matemática e que explorem as questões textuais e visuais. Por isso, reunimos algumas sugestões de atividades com materiais simples do dia a dia que você pode construir para utilizar em sala de aula a fim de trabalhar os principais conceitos da matemática.
3.2.1 Ensinando sobre Números
Ao iniciar o trabalho com números, as crianças começam a aprender os números de 1 até 10, depois vamos ampliando, do 11 ao 20, do 21 ao 30 e assim por diante, até as crianças compreenderem os números de 1 até 50 e depois de 1 até 100.
Primeiramente, as crianças precisam compreender os números. Para isso, é necessário que o professor mostre os números, explique sobre eles, mostre a quantidade de dedos das mãos que representa a mesma quantidade do número e apresente os sinais dos números em Libras.
Figura 3 - Apresentação dos números

Fonte: recurso da autora (2025)
É importante mostrar o número 1 e então pegar um objeto e explicar, isso é um. Depois mostrar o número 2 e pegar dois objetos e explicar: isso é dois. Mostrar o número 3, pegar três objetos e contar até três. E assim por diante, inicialmente até 10, ampliando a quantidade conforme as crianças forem compreendendo.
É também necessário que as crianças saibam o nome dos números e aprendam a contar nos dedos:
1 - UM, 2 - DOIS, 3 - TRÊS, 4 - QUATRO…
O professor pode propor algumas atividades lúdicas para trabalhar com os números. Por exemplo: A criança pode desenhar as duas mãos em uma folha de papel e colocar os números em cada dedo, contando de 1 até 10.
Outra sugestão é brincar mostrando os dedos das mãos para que a criança identifique a quantidade de dedos e o número que representa essa quantia.
É possível também organizar um cartaz e colocar a figura da mão com os dedos representando a quantidade. Então, a criança precisa pegar os números e colar no local correto, conforme mostra a Figura 4.
Figura 4 - Cartaz para trabalhar os números

Fonte: recurso da autora (2025)
Durante a atividade o professor pode explicar sobre a utilização dos números na sociedade. Os números são utilizados para olhar as horas no relógio, para identificar o número das casas em uma rua, a placa dos carros, os números de telefone etc.
Outra atividade possível para o trabalho com números é utilizando palitos de picolé. Primeiramente o professor construirá uma régua com os números de 0 a 10 e pintará, nos palitos de picolé, bolinhas para representar a quantidade, também de 0 a 10, conforme mostra a figura 5.
Figura 5 - Números e quantidades

Fonte: recurso da autora (2025)
Na régua dos números, a criança deverá colocar o palito que tem a quantidade de bolinhas conforme o número que está representado na régua. Esse material pode ser construído com o auxílio das crianças que, primeiramente ajudam o professor a produzir a régua e os palitos com as bolinhas e, na sequência, podem brincar e aprender números e quantidades.
Em uma outra opção de atividade, o professor pode organizar círculos de papel (ou cartolina) com os números e apresentar às crianças, mostrando o número. As crianças deverão, utilizando grampos de roupa, prender a quantidade de grampos conforme o número que está no círculo. Se o professor mostrar o círculo com o número 4, a criança deverá prender 4 grampos. Veja um exemplo na Figura 6.
Figura 6 - Atividade com números e grampos de roupa

Fonte: recurso da autora (2025)
Essas atividades podem ser utilizadas e trabalhadas diversas vezes, até as crianças entenderem o conceito dos números e conseguirem relacionar os números às quantidades.
Além dessas ideias que apresentamos, você também pode construir outras propostas de atividades utilizando material concreto para ensinar os números.
Saiba mais
Para aprofundar seus conhecimentos sobre as questões relacionadas à escrita dos números pelas crianças surdas, sugerimos a leitura da dissertação elaborada por Márcia Cristina Amaral da Silva e intitulada A escrita numérica por crianças surdas bilíngues.
A escrita numérica por crianças surdas bilínguesConheça também o livro infantil Eu, vovô e os números, que você pode ler para as crianças e explorar nas aulas. Nesse livro, um menino aprende a contar de forma divertida enquanto passeia com o avô pelo sítio da família. Com ilustrações encantadoras, os números surgem naturalmente das formas da natureza e do cotidiano.
Eu, vovô e os números3.2.2 Sistema de Numeração Decimal
Explicar para as crianças o que é a numeração decimal e também o que significa é importante para o aprendizado da matemática.
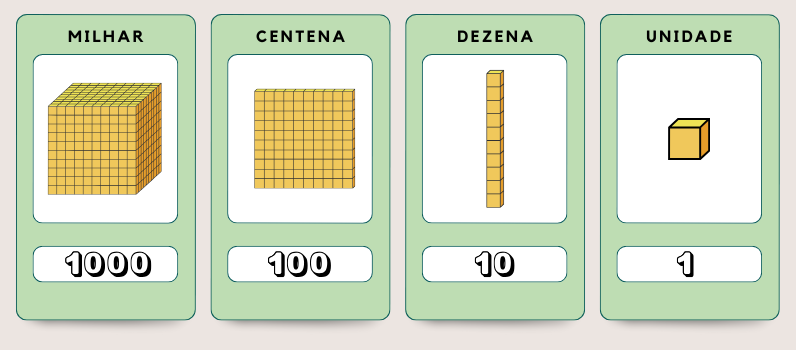
Para explicar o que é UNIDADE, DEZENA e CENTENA, o professor pode mostrar imagens, utilizar o ábaco ou o material dourado.
No material dourado, o professor mostra uma unidade, duas unidades, três unidades e assim por diante até dez unidades. Quando tem dez unidades, mostra que as 10 unidades representam a mesma quantidade da DEZENA e explica: 10 unidades é igual a 1 dezena.
Depois mostra que 10 dezenas formam 1 CENTENA e que a centena é igual a cem.
Figura 7 - Material Dourado
Fonte: Equipe de design (2025)
Para as crianças compreenderem, talvez seja necessário o professor explicar várias vezes e perguntar:
UNIDADE é igual ao quê?
Unidade é igual a um.
DEZENA é igual ao quê?
Dezena igual a dez.
CENTENA é igual ao quê?
Centena é igual a cem.
Outro recurso que o professor pode utilizar para trabalhar os conceitos de UNIDADE, DEZENA e CENTENA é o ábaco. Com o ábaco as crianças conseguem contar as unidades e, em seguida, o professor pode então explicar que dez unidades formam uma dezena. Como os materiais são coloridos, chamam a atenção da criança e ajudam a aprender de forma lúdica.
Figura 8 - Ábaco

Fonte: Equipe de design (2025)
Após explicar os conceitos de unidade, dezena e centena, tanto com o ábaco quanto com o material dourado e de permitir que as crianças manuseiem esses materiais, o professor pode propor algumas atividades para a sistematização dos conceitos.
Apresentamos abaixo algumas sugestões de atividades:
Figura 9 - Atividades com material dourado
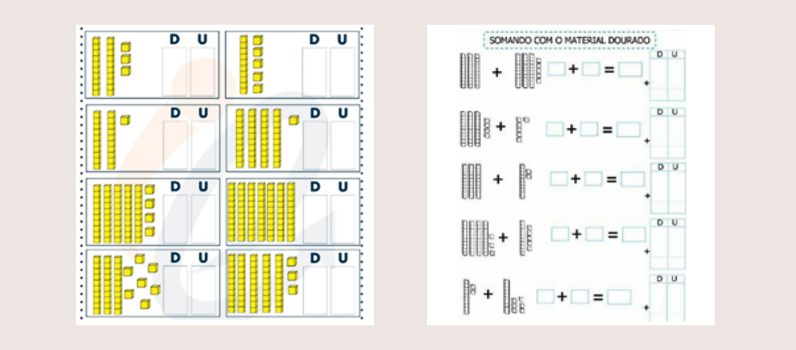
Fonte: recurso da autora (2025)
Figura 10 - Atividades com ábaco

Fonte: recurso da autora (2025)
Saiba mais
Um trabalho interessante realizado com crianças surdas e que remete a representação do número e sua apropriação do sistema de numeração decimal pelas crianças surdas, foi elaborado pelas autoras Maria Emília Zanquetta e Clélia Maria Nogueira, intitulado Uma investigação com alunos surdos do ensino fundamental: o cálculo mental em questão.
Nessa pesquisa as autoras propuseram diversas atividades e chegaram a algumas conclusões que valem a leitura do artigo completo. As atividades propostas destacam as possibilidades do uso da Libras em sala de aula, sem ser apenas uma interpretação de aulas tradicionais de matemática, mas de forma a favorecer o desenvolvimento cognitivo através de uma metodologia dialógica em Libras, para crianças surdas.
Uma investigação com alunos surdos do ensino fundamental3.2.3 Ensinando Adição
Na explicação sobre a adição, é importante que o professor apresente para as crianças o que é a adição e que, em Matemática, utiliza-se o símbolo + para representar uma adição. Explicar primeiro utilizando os números de 1 até 10. Sugerimos uma atividade utilizando um cabide e prendedores de roupa, conforme mostra a Figura 11.
Figura 11 - Atividade de adição com cabide e grampos de roupa

Fonte: recurso da autora (2025)
No centro do cabide, insere o sinal de + (adição). A criança vai jogar o dado e, conforme o número que cair, precisa colocar os prendedores no lado esquerdo do cabide. Depois, joga novamente o dado e coloca a quantidade de prendedores no lado direito do cabide. Então, vai contar quantos prendedores tem no cabide, fazer a soma e registrar o total de prendedores.
Durante a brincadeira é importante que o professor incentive a criança a falar ou sinalizar o número total de prendedores. A criança pode brincar várias vezes, utilizando os números até 10 e, após cada rodada, fazer o registro das operações de adição no caderno.
Outra sugestão de atividade é com copos de plástico e palitos coloridos. O professor precisa elaborar etiquetas com operações de adição, com resultado até 10, e colar nos copos plásticos, conforme mostra a figura 12.
Figura 12 - Atividade de adição com copos plásticos

Fonte: recurso da autora (2025)
Então, precisa explicar para as crianças que elas precisarão pegar a quantidade de palitos coloridos, conforme os números que estão na etiqueta colada no copo. Por exemplo: no copo com a etiqueta 3 + 4, a criança precisará pegar 3 palitos de uma cor e mais 4 palitos de outra cor, colocando-os dentro do copo. Então, vai somar para ver qual é o número total de palitos no copo.
O professor pode mostrar inicialmente um exemplo, pegar o copo plástico, colocar os palitos e explicar para as crianças. No copo onde está a operação 2 + 2, o professor pode pegar 2 palitos vermelhos e 2 palitos azuis, e explicar que a adição é a soma dos dois palitos vermelhos com os dois palitos azuis e que registramos: 2 + 2 = 4.
Para essa atividade, ao invés de palitos, podem ser utilizadas tampinhas coloridas, bolinhas, peças de encaixar, dentre outros materiais que o professor tenha disponível. O importante é trabalhar com o material concreto, pois a criança pode manusear e entender melhor.
Na figura 13 mostramos um exemplo de atividade utilizando peças de encaixar coloridas. O professor pode organizar operações de adição em uma folha de papel e pedir que as crianças peguem a quantidade de peças conforme a operação que está no papel.
Figura 13 - Operação de adição com peças de encaixar
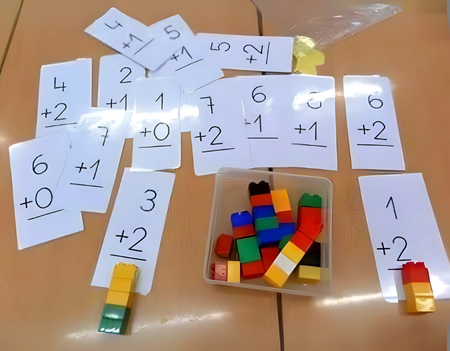
Fonte: recurso da autora (2025)
Por exemplo: 3 + 2. A criança precisará pegar 3 peças de uma cor e mais 2 peças de outra cor, então, vai contar e vai somar a quantidade total de peças, registrando o número 5 como resultado da adição.
O professor pode propor para a criança brincar diversas vezes, realizando várias operações diferentes. Assim, de forma lúdica, vai internalizando o conceito de adição.
Também é possível trabalhar a adição utilizando peças de dominó. O professor pega uma peça de dominó, coloca na vertical e pede para a criança fazer a soma dos números, conforme mostra a figura 14.
Figura 14 - Adição com peças de dominó

Fonte: atividades para educação (2014)
Por exemplo, ao pegar a peça do dominó que tem os números 5 + 1, a criança precisará fazer a soma e responder qual é o total de bolinhas que temos na peça. Importante fazer essa atividade várias vezes, utilizando peças diferentes para que a criança consiga compreender e desenvolver melhor o conceito de adição.
3.2.4 Ensinando Subtração
Depois de explicar sobre o conceito de adição, agora vamos trabalhar o conceito subtração. Importante começar relembrando com as crianças os números e também o que aprenderam sobre a adição, que é a soma de quantidades.
Depois disso, o professor vai explicar que a subtração é uma operação básica da Matemática e que é a operação inversa da adição. Subtrair é retirar uma quantidade ou porção, de algo, de uma coleção ou conjunto. Ao separar e retirar uma parte de um todo, estamos subtraindo. Na linguagem matemática, o símbolo para subtração é um traço ( - ) e lemos: menos.
É importante explicar para as crianças que adição e subtração são diferentes. Adição é soma, ou seja, eu adiciono uma quantidade. A subtração é menos, é tirar ou reduzir uma quantidade.
O professor pode começar explicando a subtração utilizando os dedos das mãos. Por exemplo: mostrar 7 dedos e esconder 3 dedos e então perguntar para as crianças: quantos sobraram? Também pode exemplificar utilizando palitos de picolé: mostra 8 palitos de picolé e tira 4 palitos. Quantos palitos sobraram? Pedir que as crianças façam a operação de subtração e encontrem os resultados nos exemplos apresentados pelo professor.
Uma atividade que o professor pode realizar com as crianças está ilustrada no exemplo abaixo.
Figura 15 - subtração utilizando imagens das mãos
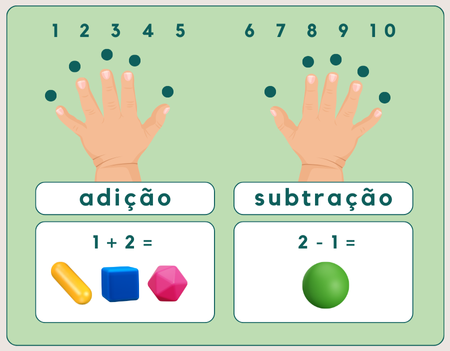
Fonte: Equipe de design (2025)
Essa atividade apresenta a mão com os dedos e as operações de adição e de subtração. O professor pode mostrar a diferença entre a adição e a subtração para que as crianças compreendam a diferença.
Agora vamos ver alguns exemplos para elaborar atividades nas quais a criança poderá compreender o conceito de subtração através de brincadeiras e atividades práticas.
Uma possibilidade é utilizar atividades que apresentem imagens dos dedos das mãos, a partir das quais a criança poderá utilizar seus dedos para resolver. Observe a figura abaixo:
Figura 16 - Atividade de subtração com desenho dos dedos
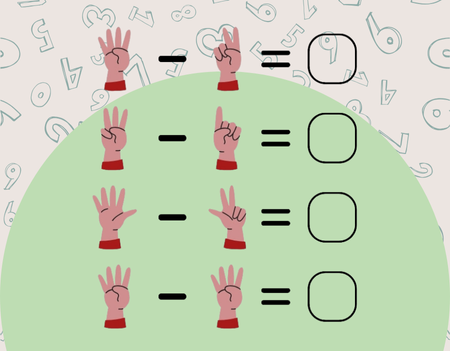
Fonte: Equipe de design (2025)
No primeiro exemplo, temos uma mão com 4 dedos e então precisamos tirar (ou esconder) 2 dedos. Então, quantos dedos ficaram na mão? A resposta é 2 dedos.
Também é possível fazer essa mesma atividade com objetos ou com imagem de alimentos, conforme mostra a figura 17.
Figura 17 - Atividade de subtração com alimentos
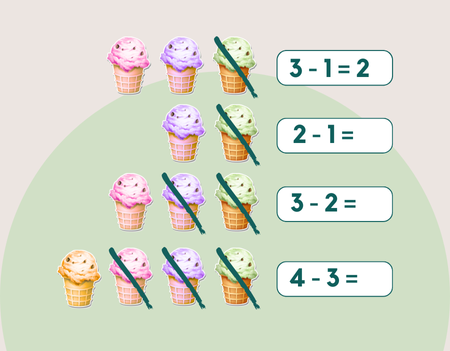
Fonte: Equipe de design (2025)
Nesse exemplo, além do desenho do alimento, há também os números. Então, o professor pode explicar: eu tenho três sorvetes e comi um sorvete. Precisa explicar que vai sempre tirar o último número (1) e não o primeiro (3). Se eu tinha três e comi um, sobraram dois. Agora eu tenho 2 sorvetes.
Na atividade em papel a criança pode usar o lápis para sublinhar ou riscar a imagem do alimento que foi comido, indicando que foi tirado ou subtraído.
3.2.5 Ensinando Multiplicação
Depois de a criança aprender sobre os números, sobre a adição e a subtração, começará a aprender a multiplicação e vai conhecer a tabuada. É importante explicar que para a multiplicação, vamos utilizar a adição. O professor vai explicar, inicialmente, a tabuada usando a adição.
Por exemplo: 2 x 4 = ?
Precisa explicar que é duas vezes o número quatro, ou seja, 4 + 4. E então a criança vai calcular.
Para mostrar esse exemplo de maneira concreta, o professor pode utilizar dois pratos e colocar quatro bananas no primeiro prato e mais quatro bananas no segundo prato. Dois pratos com quatro bananas em cada prato e então perguntar para a criança: quantas bananas temos no total?
Figura 18 - Exemplo da multiplicação 2 x 4

Fonte: Equipe de design (2025)
Na sequência é possível mostrar para a criança que a operação 4 x 2 terá uma representação diferente, mas com o mesmo resultado. Nesse exemplo, será necessário quatro pratos, com duas bananas em cada prato.
Figura 19 - Exemplo da multiplicação 4 x 2

Fonte: Equipe de design (2025)
Outra forma de explicar a multiplicação para as crianças é utilizando um cartaz. No cartaz o professor vai colocar os números: 1x1, 2x2, 3x3, 4x4…até o 9x9 e colocar, ao lado dos números, a quantidade de copos: 1, 2, 3… até 9. Na lateral, fazer um suporte para colocar: palitos de picolé, canudinhos, tampinhas, clips ou outros materiais, para que a criança possa pegar e contar.
Figura 20 - Cartaz da multiplicação

Fonte: Pinterest (Moisés, s.d.)
A criança vai pegar os palitos e colocar a quantidade dentro de cada copo. Por fim, vai contar quantos palitos tem e então registrar no caderno.
Saiba mais
Para aprofundar seus conhecimentos e complementar a parte teórica que o professor precisa dominar, sugerimos, os vídeos em Libras (com áudio e legenda em português) do curso de Metodologia de Ensino de Matemática do INES - Instituto Nacional de Educação de Surdos.
Recomendamos especialmente o terceiro vídeo que trata das estruturas aditivas e multiplicativas que envolvem os problemas de matemática. Esse conhecimento o ajudará a entender mais claramente como ensinar aos alunos a resolverem os problemas, estabelecendo relações com o que propõe a BNCC.
Vídeo: Estruturas aditivas e multiplicativas na matemática3.2.6 Ensinando Divisão
Depois que a criança já compreendeu a adição, a subtração e a multiplicação, vamos trabalhar então o conceito de divisão, consolidando assim, a aprendizagem das quatro operações básicas da matemática.
Primeiramente, o professor precisa explicar o que é a divisão. É uma operação matemática na qual repartimos números ou objetos em partes iguais.
Na sequência, exemplificar a divisão: 9 ÷ 3 = ?
O professor vai pegar 9 bananas e 3 pratos e mostrar para a criança que precisa dividir as 9 bananas nos 3 pratos de forma igual. Então primeiramente coloca uma banana em cada prato e pergunta para criança se ainda tem bananas para dividir. Então, coloca mais uma banana em cada prato e, por fim, mais uma banana em cada prato. Pergunta para as crianças: quantas bananas temos em cada prato?
Figura 21 - Exemplo de divisão

Fonte: Equipe de design (2025)
Outra forma de explicar a divisão é utilizando cartelas com imagens. No exemplo a seguir temos cartelas com as imagens e, logo abaixo, a operação de divisão. Na primeira cartela, podemos observar a imagem de 9 ossos e 3 cachorros, com a operação: 9 ÷ 3 = ?
Figura 22 - Cartelas para trabalhar a divisão
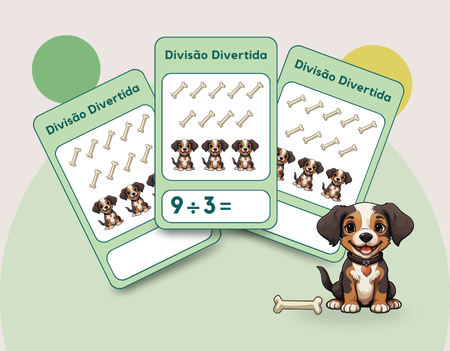
Fonte: equipe design (2025)
A criança pode circular a quantidade de ossos que cada cachorro vai poder comer ou então, ligar cada osso ao cachorro e contar quantos ossos cada um recebeu. Há várias possibilidades para o professor explicar e explorar com as crianças.
Saiba mais
No artigo Atividades Pedagógicas no Ensino Fundamental para Alunos Surdos: produção de material didático de Matemática para uma prática docente bilíngue, dos autores Willian Silva de Oliveira e Renata Barbosa Dionysio, você vai encontrar uma proposta de aplicação de materiais didáticos de matemática com crianças surdas, relacionando com a BNCC e apresentando os resultados obtidos pelos autores no decorrer da utilização do material.
Atividades Pedagógicas no Ensino Fundamental para Alunos Surdos3.2.7 Ensinando as Horas
Outro assunto importante para trabalharmos em matemática é sobre a contagem do tempo e sobre a marcação das horas.
O professor pode começar perguntando para as crianças como elas sabem quando é hora de comer, de dormir, de brincar no parque, de ir para a escola?
Explicar que o ser humano desenvolveu a noção de “hora” observando os fenômenos naturais, especialmente a posição do Sol. A partir disso, foram criados os primeiros relógios e o dia foi dividido em 24 partes, sendo que cada parte corresponde a 1 hora e cada hora tem 60 minutos.
Para saber que horas são, nós utilizamos o relógio. No relógio analógico temos os números de 1 até 12. No relógio digital, podemos ver as horas de 1 até 12 ou de 1 até 24. Importante explicar para as crianças os diferentes tipos de relógio e as diferentes formas de ver as horas.
Figura 23 - Relógio analógico

Fonte: Equipe de design (2025)
Com o relógio analógico, o professor pode mostrar o relógio para os alunos, mostrar que há dois ponteiros, um maior e um menor. O ponteiro menor marca as horas e o ponteiro maior marca os minutos.
Pode colocar o relógio no quadro e fazer perguntas para as crianças, por exemplo: que horas a aula começa? Que horas é o lanche? Que horas a aula termina? Que horas você acorda? Que horas você vai dormir? E então chama uma criança para marcar no relógio a resposta para cada pergunta.
Para registrar essa atividade, o professor pode entregar para cada criança uma folha com o desenho do relógio analógico e, a cada pergunta que foi trabalhada no quadro, a criança registra a resposta no relógio que está na folha, desenhando os ponteiros e anotando, no espaço abaixo do relógio, as horas no formato digital.
Figura 24 - Atividade para registro das horas

Fonte: equipe design (2025)
O professor também pode propor que as crianças construam o seu próprio relógio para então utilizá-lo no desenvolvimento de diferentes atividades nas aulas de matemática. Com o relógio, as crianças podem manusear os ponteiros e aprender a identificar as horas.
Assista ao vídeo e veja como você pode construir um relógio analógico para trabalhar o conceito de horas e minutos com as crianças.
Para que as crianças compreendam o conceito de minutos e entendam que cada hora possui 60 minutos, você pode inserir a marcação dos minutos ao redor do relógio e então explicar como identificamos o horário.
Por exemplo:
1) duas horas e dez minutos: o ponteiro menor estará no dois e o maior também estará no dois, pois ali é onde registramos 10 minutos.
2) cinco horas e cinquenta e cinco minutos: o ponteiro menor estará no cinco e o maior estará no onze, que é onde registramos 55 minutos.
Figura 25 - Relógio analógico com a marcação dos minutos

Fonte: recurso da autora (2025)
Saiba mais
Para explicar o conceito de tempo, das horas e minutos, sugerimos alguns livros de literatura infantil que abordam essa temática e que você poderá utilizar para introduzir o assunto com os alunos ou mesmo para instigá-los a querer saber mais.
O tempo que o tempo tem - Autora: Efigênia Alves
O livro conta a história de uma menina que tenta entender o que é tempo através de perguntas feitas a adultos de diferentes idades. Ela anota as respostas que descrevem o tempo de diferentes maneiras. Aprende sobre o relógio e o calendário, além de conhecimentos temporais como ontem, antigamente, ano passado. Por fim, a menina conclui que ninguém sabe o tempo que o tempo tem.
O tempo que o tempo temO Menino e o Tempo - Autora: Fabiana Guimarães
A hora é o pedacinho de tempo para fazer as coisas. Zito vivia perdendo a hora de ir para aula, de fazer as tarefas, de almoçar, de tomar banho… Sua mãe ficava brava e ele ficava triste, por nunca alcançar o tempo.
O Menino e o TempoO Relógio que Perdeu a Hora - Autor: Flávio Colombini
O Relógio Que Perdeu a Hora conta a história de um relógio que, quando despertou, reparou que tinha perdido a hora. Então, ele saiu procurando a hora pelo mundo afora. É um livro muito divertido, escrito em poesia narrativa e cheio de rimas.
O Relógio que Perdeu a HoraO Tempo de Nino - Autora: Karine Portela
Nino sempre estava atrasado até ganhar um relógio de presente. Descobre que pode controlar os ponteiros e mudar o tempo a seu favor. Uma história divertida sobre aprendizado e organização para crianças, incentivando a autonomia e a noção de responsabilidade.
O Tempo de NinoMarcelo: de hora em hora - Autora: Ruth Rocha
Neste livro as crianças vão aprender, junto com o Marcelo, uma forma divertida de ver as horas, além de entender como e por que as pessoas dividem o tempo em pedacinhos. O livro também traz sugestões de atividades e brincadeiras que o professor pode realizar com as crianças.
Marcelo: de hora em horaO tempo - Autor: Ivo Minkovicius
O tempo foge e passa sem parar. Vai para o passado em lembranças que ficam guardadas dentro de nós. Registra o agora, que também passa bem depressa e logo vira futuro. O tempo vira passado e futuro num instante. E não para um minuto, nem um segundo! Esse livro mostra, com graça e muita sutileza, as formas que o tempo encontra para fazer o mundo acontecer.
O tempoQuem Quer Matar o Tempo? - Autora: Miriam Portela
O que fazer quando o Tempo – um rei tão bom que quase todos querem o seu bem – sofre um atentado? Pois é, isso aconteceu. E lá foi o Dia, acordado antes da hora por algumas aves que tinham o dom da fala, descobrir o que havia ocorrido e investigar quem era capaz de tamanha maldade.
Quem Quer Matar o Tempo?4. Uso de tecnologias educacionais para o ensino da matemática
Em sua essência, a tecnologia refere-se a um conjunto de conhecimentos, técnicas, ferramentas e processos que buscam solucionar problemas, facilitar e criar novos produtos e aprimorar as atividades dos sujeitos.
Segundo Kenski (2012) a tecnologia refere-se ao conjunto de diferentes saberes e fundamentos científicos voltados para planejar, construir e utilizar ferramentas úteis para determinado tipo de atividade que se deseja desempenhar.
“As tecnologias - velhas, como a escrita, ou novas, como as agendas eletrônicas - transformam o modo como dispomos, compreendemos e representamos o tempo e o espaço à nossa volta. [...]” (Kenski, 1998, p.60). Essa perspectiva revela que a tecnologia hoje não é a mesma de décadas atrás, que o novo e moderno agora, possivelmente será ultrapassado daqui há algumas décadas.
Atualmente, estamos vivendo a era digital, em que a internet dominou e se tornou fundamental nas escolas, empresas e residências. O mundo está evoluindo, nossa percepção e compreensão do mundo também. A cada dia novas formas de aprender e de utilizar os conhecimentos se mostram promissores e as novas tecnologias têm demonstrado isso.
No que tange à educação, as tecnologias são os meios utilizados pelo docente durante todo o processo pedagógico que introduz mudanças significativas na maneira de organizar o ensino a fim de promover a mediação entre o professor, o conteúdo ensinado e a compreensão do aluno sobre o assunto (Kenski, 2012).

Alinhada às diretrizes da Base Nacional Comum Curricular (BNCC), as tecnologias podem contribuir significativamente no estudo da Matemática, “[...] para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados” (Brasil, 2018, p.267).
Tendo em vista que a sociedade está em constante transformação e que as tecnologias fazem parte deste processo, a BNCC destaca “[...] o uso de tecnologias – como calculadoras, para avaliar e comparar resultados, e planilhas eletrônicas, que ajudam na construção de gráficos e nos cálculos das medidas de tendência central” (Brasil, 2018, p.274).
De acordo com Moran (2017), primeiramente é preciso identificar quais tipos de tecnologias são mais adequadas para determinado estudo e, em seguida, deve se ter o domínio técnico-pedagógico para utilizar tais tecnologias na construção do conhecimento.
4.1 Recursos tecnológicos no ensino de matemática
Diversas tecnologias são interessantes para o ensino de matemática nos anos iniciais do Ensino Fundamental.
Destacamos os jogos digitais e os aplicativos com foco educacional, as plataformas de aprendizagem, softwares educacionais como o GeoGebra, que trabalha conceitos numéricos e geométricos, além dos recursos de realidade virtual e aumentada, das ferramentas de organização de dados e dos recursos de Robótica Educacional.
Conheça alguns desses recursos:
Jogos digitais, aplicativos educativos e plataformas de aprendizagem: apresentam desafios e atividades lúdicas. Podem ser utilizados tanto para apresentar novos conteúdos, quanto para revisar o que as crianças já aprenderam. Exemplos: Mentalidades Matemáticas; Khan Academy; Matific.
Software de Geometria: trabalha conceitos geométricos, algébricos e numéricos, permitindo que os alunos investiguem problemas matemáticos de forma concreta, dinâmica e interativa. Exemplo: Geogebra.
Softwares de programação: as crianças exploram conceitos de geometria, álgebra e estatística criando seus próprios jogos e animações. Assim, desenvolvem o raciocínio lógico, a criatividade e a autonomia. Exemplo: Scratch.
Realidade Virtual e Aumentada: facilitam a compreensão de conceitos abstratos, pois proporcionam experiências imersivas e a visualização de objetos matemáticos em 3D.
Ferramentas de organização de dados: auxiliam na coleta, organização e análise de dados, permitindo que os alunos desenvolvam competências de interpretação e resolução de problemas.
Recursos de Robótica Educacional: auxiliam no aprendizado através da construção e da programação, desenvolvendo o raciocínio lógico e a resolução de problemas.
Também precisamos destacar os recursos tecnológicos visuais disponibilizados por meio de videoaulas. Especialmente para o trabalho com crianças surdas, os vídeos são recursos importantes para apresentar conceitos matemáticos de forma visual, atrativa e interativa.
Saiba mais
O canal Jovens Notáveis, no YouTube, oferece conteúdos educativos de forma lúdica para crianças e jovens seguindo as orientações da Base Nacional Comum Curricular (BNCC). Possui uma playlist com vídeos traduzidos para Libras nas áreas de Matemática, Ciências e Língua Portuguesa.
Jovens NotáveisO canal Fundamental para todos, no YouTube, tem como objetivo utilizar a Libras como língua de instrução e apresentar conteúdos imagéticos para crianças do Ensino Fundamental em diversas áreas. Destacamos a playlist Matemática em Libras com vídeos que explicam conteúdos da área de Matemática para crianças.
Playlist Matemática em Libras4.1.1 Vídeos em Libras com conteúdos de matemática
O INES – Instituto Nacional de Educação de Surdos, disponibiliza em seu canal do YouTube uma série de vídeos em Libras, com áudio e legenda em português, produzidos pela TV INES. Alguns desses vídeos não só podem, como devem, ser utilizados em sala de aula, principalmente em aulas de matemática para jovens e adultos surdos.
Canal TV INESNo Canal da TV INES você encontra o programa A vida em Libras que apresenta diferentes situações do cotidiano e os sinais em Libras. Nesse programa há um episódio chamado Matemática, que apresenta de maneira ilustrada os sinais referentes à Matemática, desde aqueles que usamos na escola, como somar, subtrair, multiplicar, dividir, regra de três, até aplicações dessa disciplina no dia a dia, como juros, porcentagem, área e metro quadrado.
Playlist A vida em Libras Episódio MatemáticaOutros episódios desse mesmo programa não ensinam diretamente conteúdos ou sinais de matemática, mas podem ser utilizados para introduzir e motivar o estudo de assuntos do dia a dia relacionados com a matemática. Por exemplo, para falar do Sistema Monetário, seguem algumas sugestões de vídeos:
Supermercado I e II
No primeiro episódio os apresentadores vão às compras e mostram os sinais de alimentos como feijão, arroz, diversos tipos de carne, queijo, azeite, macarrão, entre outros itens do carrinho de compras.
Depois de comprar os alimentos, no segundo episódio, é hora de comprar bebidas como: água, refrigerante, sucos, cerveja e vinho e de estocar materiais de limpeza e higiene, como: álcool, desinfetante, sabão em pó, detergente, shampoo, sabonete e condicionador.
Vídeo Supermercado I Vídeo Supermercado IICasa da Moeda, Dinheiro e Imposto de Renda
No vídeo sobre a Casa da Moeda, o apresentador vai conhecer como o dinheiro é fabricado e como funcionam as máquinas que produzem as moedas. Explica quais são as regras para emitir notas de dinheiro e mostra que a Casa da Moeda imprime também diplomas e passaportes, além de ter produzido as medalhas olímpicas e paralímpicas do Rio 2016.
No vídeo sobre o dinheiro, são apresentados os vocabulários relacionados ao dinheiro, como: banco, cartões de débito e crédito, cheque, poupança, taxa, juro, saque, salário, entre outros, além de explicar como funciona a fabricação do dinheiro e sua distribuição.
No vídeo sobre o Imposto de Renda, são ensinados os vocabulários relacionados a esse tema, além da explicação sobre como declarar o IRPF - Imposto de Renda de Pessoas Físicas, quando ele foi criado e porque o imposto existe.
Vídeo Casa da Moeda Vídeo Dinheiro Vídeo Imposto de RendaAlém dos vídeos mais específicos da área da matemática, no canal da TV INES no YouTube você pode encontrar outros vídeos que integram conhecimentos matemáticos com assuntos de outras disciplinas, como, por exemplo, o vídeo sobre períodos de tempo em Libras, que faz parte da coleção Aulas de Libras.
Vídeo Período de tempo em LibrasNo programa De olho na Ciência você também encontra vídeos que abordam sobre a temática tempo e sua relação com temas ambientais, como o tempo para a decomposição de resíduos, que exige a compreensão dos números. Com esses materiais é possível promover uma abordagem interdisciplinar, integrando conteúdos de diferentes áreas do conhecimento.
No vídeo A produção de lixo e seus impactos - parte 1, os personagens abordam sobre a produção de resíduos, discutem sobre o gerenciamento do lixo gerado e incentivam a reciclagem, auxiliando na formação de sujeitos mais conscientes.
Na segunda parte do vídeo, os personagens explicam quanto tempo o lixo leva para se decompor na natureza, discutem a produção de lixo e seus impactos, e apresentam o princípio dos três ‘R’: “Reduzir”, “Reutilizar” e “Reciclar”.
A produção de lixo e seus impactos - parte 1 A produção de lixo e seus impactos - parte 24.1.2 Glossários em Libras na área da Matemática
Não há muitos glossários com termos específicos da área de matemática. Há uma urgência para que sinais específicos dessa área sejam organizados, produzidos, unificados e divulgados para que o estudo dessa ciência pelos surdos se aprofunde nos conceitos mais abstratos com mais facilidade e propriedade.
O Calculibras, desenvolvido pelo professor Danilo Carvalho, é um glossário com foco nos termos da Geometria Plana e seus complementos algébricos.
CalculibrasO Inep - Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira - disponibilizou em seu canal no YouTube um glossário de Matemática e suas Tecnologias para as provas do Enem de 2017 e 2018. Vale a pena conferir!
Glossário de Matemática do InepOutro exemplo de glossário em Libras na área de matemática foi produzido por Rodolpho Pinheiro D’Azevedo em sua dissertação de mestrado na Universidade de Brasília (Unb), em 2019.
Glossário Matemática em LibrasEncontramos também o sinalário disciplinar em Libras, que foi elaborado pela Secretaria do Estado da Educação do Paraná em parceria com o CAS - Centros de Apoio ao Surdo e aos Profissionais da Educação de Surdos do Paraná, com o objetivo de alcançar os profissionais da educação, estudantes surdos e a comunidade surda.
O sinalário está organizado por áreas do conhecimento, sendo uma delas a matemática.
Sinalário PR - MatemáticaO canal MathLibras, além de vídeos com conteúdos na área da matemática, apresenta também um pequeno glossário com termos de matemática que são utilizados nos vídeos.
Glossário MathLibrasÉ claro que esses não são os únicos vídeos com aulas de matemática em Libras ou com glossários de matemática disponíveis na internet. No entanto, tivemos o cuidado de indicar aqueles que são referendados por pesquisadores e instituições de referência e credibilidade.
Considerações Finais
Chegamos ao final dos estudos sobre os conceitos matemáticos e as metodologias para ensinar crianças surdas.
Nesse módulo você conheceu conteúdos da área de matemática que são trabalhados na educação infantil e nos anos iniciais. Também se apropriou de metodologias e recursos que podem ser utilizados para tornar as aulas mais lúdicas, visuais e concretas.
Esse conhecimento é importante para que você possa planejar atividades interativas e que utilizam recursos visuais, materiais atrativos e interessantes para o público infantil.
Por fim, você conheceu algumas tecnologias que podem auxiliar na aprendizagem da matemática e tornar essa área do conhecimento mais dinâmica e interessante para as crianças.
Esperamos que todos esses conhecimentos sejam úteis na sua trajetória de aprendizagem e também na sua atuação profissional.
Referências
BOALER, Jo. Mentalidades matemáticas: estimulando o potencial dos estudantes por meio da matemática criativa, das mensagens inspiradoras e do ensino inovador. Porto Alegre: Penso, 2018.
BOALER, Jo. Mente sem barreiras: as chaves para destravar seu potencial ilimitado de aprendizagem. Porto Alegre: Penso, 2020.
BRASIL. Base Nacional Comum Curricular. Brasília: MEC, 2018.
BRASIL. Resolução n.5, de 17 de dezembro de 2009. Fixa as Diretrizes Curriculares Nacionais para a Educação Infantil. 2009. Disponível em: https://portal.mec.gov.br/index.php?option=com_docman&view=download&alias=2298-rceb005-09&category_slug=dezembro-2009-pdf&Itemid=30192. Acesso em: 05 set. 2025.
CAMPOS, Lívia Rezende Miranda; OLIVEIRA, Guilherme Saramago de. Ensino de Matemática para surdos: um estudo sobre as metodologias. In: ENEMI - Encontro Nacional de Educação Matemática Inclusiva, 2., 2020, on-line. Anais eletrônicos [...]. Disponível em: https://www.sbembrasil.org.br/ocs/index.php/ENEMI/ENEMI2020/paper/ viewFile/1280/1258. Acesso em: 06 set. 2025.
KAMII, Constance. A criança e o número: Implicações educacionais da teoria de Piaget para a atuação com escolares de 4 a 6 anos. 39. ed. Campinas, SP: Papirus, 2015.
KENSKI, Vani Moreira. Educação e Tecnologias: o novo ritmo da informação. 8.ed. Campinas, SP: Papirus, 2012.
KENSKI, Vani Moreira. Novas tecnologias: o redimensionamento do espaço e do tempo e os impactos no trabalho docente. Revista Brasileira de Educação, n. 8, p. 58-71, maio/ago. 1998. Disponível em: http://educa.fcc.org.br/pdf/rbedu/n08/n08a06.pdf. Acesso em: 11 set. 2025.
MORAN, José Manuel. A educação que desejamos: novos desafios e como chegar lá. Campinas/SP: Papirus, 2017.
NOGUEIRA, Clélia Maria. Ignatius; BORGES, Fábio Alexandre; FRIZZARINI, Silvia Terezinha. Os surdos e a inclusão: uma análise pela via do ensino de Matemática nos Anos Iniciais do Ensino Fundamental. In: NOGUEIRA, Clélia Maria Ignatius (org.). Surdez, inclusão e matemática. Curitiba: CRV, 2013, p. 163-183.
OLIVEIRA, Willian Silva de; DIONYSIO, Renata Barbosa. Atividades Pedagógicas no Ensino Fundamental para Alunos Surdos: Produção de Material Didático de Matemática para uma prática docente bilíngue. Revista Educação Especial, v.36, n.1, p.1-19, 2023. Disponível em: https://periodicos.ufsm.br/educacaoespecial/article/view/70193. Acesso em: 16 ago. 2025.
PIAGET, Jean; SZEMINSKA, Alina. A gênese do número na criança. 3. ed. Rio de Janeiro: Zahar, 1981.
SILVA, João Alberto da; FREZZA, Júnior Saccon. A construção das noções de espaço e tempo nas crianças da Educação Infantil. Conjectura: filosofia e educação, [S. l.], v. 15, n. 1, 2010. Disponível em: https://sou.ucs.br/etc/revistas/index.php/conjectura/article/view/181. Acesso em: 9 jun. 2025.
SILVA, Márcia Cristina Amaral da. A escrita numérica por crianças surdas bilíngues. 226f., 2008. Dissertação (Mestrado em Educação para a Ciência e o Ensino de Matemática) - Programa de Pós Graduação em Educação para a Ciência e o Ensino de Matemática, Universidade Estadual de Maringá, Maringá, 2008.
SMOLE, Katia Stocco. Matemática na educação infantil. maio 2019. Disponível em: https://mathema.com.br/artigos/matematica-na-educacao-infantil/. Acesso em: 09 jun. 2025.
VARGAS, Rosane da C.; DORNELES, Beatriz V. Uma intervenção em contagem com duas crianças surdas. Cadernos CEDES, Campinas, v.33, n.91, p. 411-427, set./dez. 2013. Disponível em: https://www.scielo.br/j/ccedes/a/Hw9Xwzrxmz5fPm9q7HxNdGk/?lang=pt. Acesso em: 06 set. 2025.
ZANQUETTA, Maria Emília Melo Tamanini; NOGUEIRA, Clélia Maria Ignatius. Uma investigação com alunos surdos do ensino fundamental: o cálculo mental em questão. Revista Paranaense de Educação Matemática, Campo Mourão-PR, v. 6, n. 10, p. 61–89, jan./jun. 2017. Disponível em: https://periodicos.unespar.edu.br/rpem/article/view/6054. Acesso em: 5 set. 2025.
Conceitos matemáticos e metodologias para ensinar crianças surdas
|
[ Conteúdo ] |
Flávia de Almeida Pinheiro Fabricio Mahler Ramos Maria Luiza Guimarães de Melo |
|
[ Design instrucional ] |
Caroline Lengert |
|
[ Design gráfico ] |
Jennifer Patricio Candido |
|
[ Revisão Textual ] |
Ana Paula Flores |
|
[ Equipe de Tradução ] [ Tradutor de Libras Surdo ] |
Gabriel Finamore de Oliveira Nicoly Danielski dos Santos Nicolly Neves |
|
[ Equipe de Tradução ] [ Intérprete de Libras ] |
Jairo Nunes de Oliveira Neto Victor Hugo Lima Nazario Tatiane da Silva Campos [coordenadora] |
|
[ Revisão dos Vídeos em Libras ] |
Ueslei Paterno |
|
[ Edição de Vídeo ] |
Andres Leonardo Salas Garces Lincohn Santos da Rosa |
Como referenciar este livro:
PINHEIRO, Flávia de Almeida; RAMOS, Fabricio Mahler; MELO, Maria Luiza Guimarães de. Conceitos matemáticos e metodologias para ensinar crianças surdas. 2025. Disponível em: https://moodle.ifsc.edu.br/mod/book/view.php?id=355328. Acesso em: dd mmm aaaa. [material digital].

Este trabalho está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-CompartilhaIgual 4.0 Internacional.
